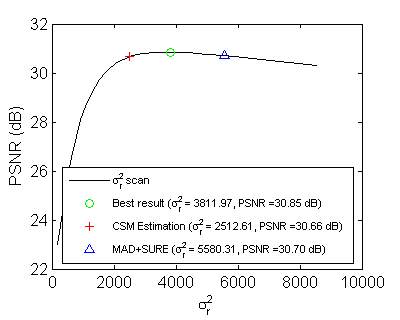
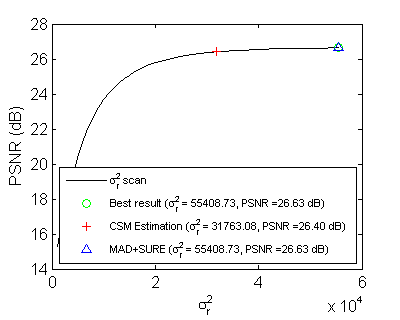
Abstract

Range-weighted neighborhood filters are useful and popular for their edge-preserving property and simplicity, but they are originally proposed as intuitive tools. Previous works needed to connect them to other tools or models for indirect property reasoning or parameter estimation. In this work, we introduce a unified empirical Bayesian framework to do both directly. A neighborhood noise model is proposed to reason and infer the Yaroslavsky, bilateral, and modified non-local means filters by joint maximum a posteriori and maximum likelihood estimation. Then the essential parameter, range variance, can be estimated via model fitting to the empirical distribution of an observable chi scale mixture variable. An algorithm based on expectation-maximization and Quasi-Newton optimization is devised to perform the model fitting efficiently. Finally, we apply this framework to the problem of color-image denoising. A recursive fitting and filtering scheme is proposed to improve the image quality. Extensive experiments are performed for a variety of configurations, including different kernel functions, filter types and support sizes, color channel numbers, and noise types. The results show that the proposed framework can fit noisy images well and the range variance can be estimated successfully and efficiently.

Publications

C.-T. Huang, "Bayesian Inference for Neighborhood Filters with Application in Denoising," IEEE Trans. Image Processing, vol. 24, no. 11, Nov 2015.
(Generalized kernels and extensive experiments)
[preprint]

C.-T. Huang, "Bayesian Inference for Neighborhood Filters with Application in Denoising," IEEE CVPR 2015.
(Basic idea on Gaussian kernel)
[paper] [supplementary proof] [poster]

Source Code

Matlab code for reproducing the results for Yaroslavsky and bilateral filters, which includes getting CSM pdf, EM+ fitting, and filtering.
[NNM_Bilateral.zip (7MB)]

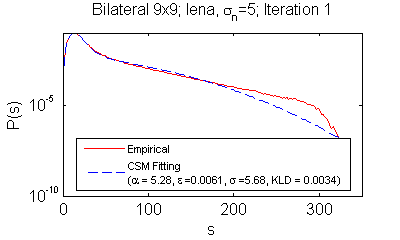
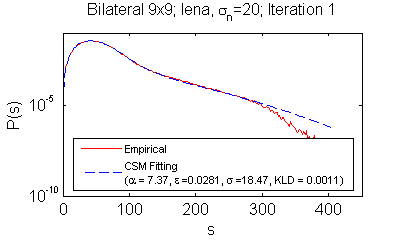
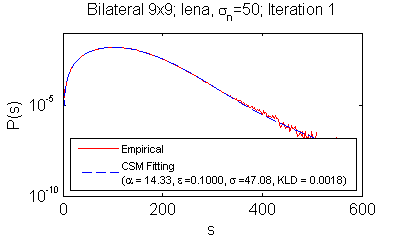
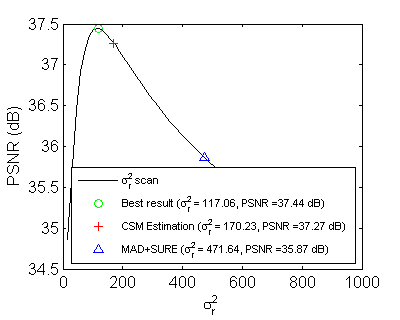
Supplementary Data for Experimental Results

Please click on the following links for the detailed fitting and filtering results:

- Yaroslavsky 5x5 filter (ϵ_bd=0.1) (ϵ_bd=1.0)

- Yaroslavsky 9x9 filter (ϵ_bd=0.1) (ϵ_bd=1.0)

- Bilateral 9x9 filter (ϵ_bd=0.1) (ϵ_bd=1.0)

- Bilateral 13x13 filter (ϵ_bd=0.1) (ϵ_bd=1.0)

- MNLM-Simple filter (ϵ_bd=0.1)

- MNLM-DCT filter (ϵ_bd=1.0)

- Bilateral 9x9 filter on Multispectral image HYDICE with selected frequency bands (k=3~9)

- Bilateral 9x9 filter with generalized kernels: (Laplacian) (GGD4) (Epanechnikov) (Biweight) (Triweight) (Uniform)

- Bilateral 9x9 filter on different noise types (Uniform/Possion/S&P)

- Natural image gradients (four-connected neighborhood) (gradient)

Note:

1. Best viewing resolution is 1920x1080. Otherwise, you may need to zoom out the webpage for a good viewing experience.
2. The original RGB image files can be found here: ori_color_images.zip.
3. The tested multispectral images can be found here: hydice_nine_bands.zip. The multispectral HYDICE image is downloaded from here, and the tested images are extracted by MultiSpec.

Acknowledgement

This work was supported by the Ministry of Science and Technology, Taiwan, R.O.C. under Grant No. MOST 103-2218-E-007-008-MY3.

Last update on Dec 7, 2015