Fast Distribution Fitting for Parameter Estimation of Range-Weighted Neighborhood Filters
Department of Electrical Engineering, National Tsing Hua University
|
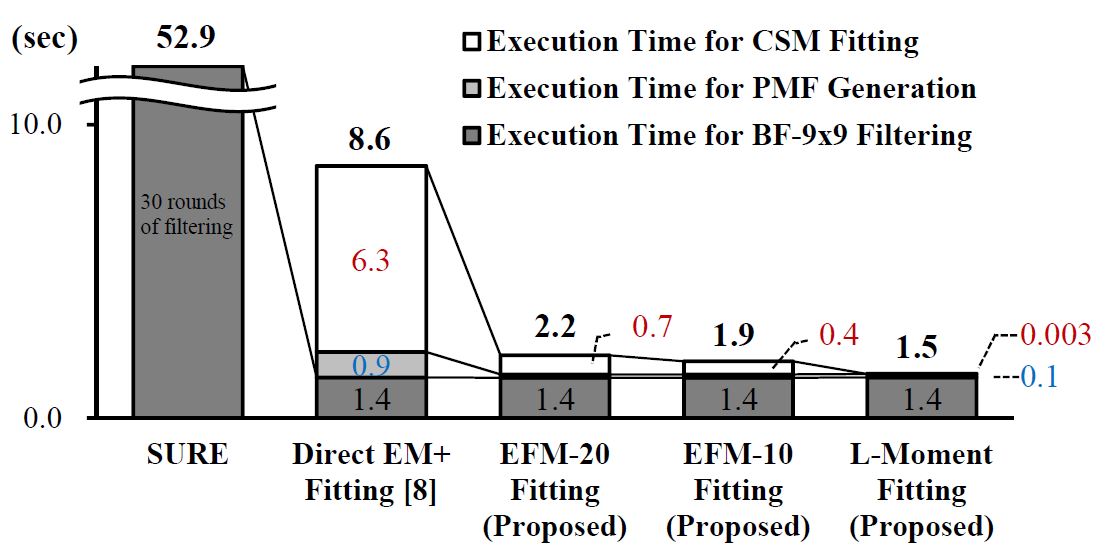
Abstract The range variance of neighborhood filters is well estimated via distribution fitting of a chi scale mixtures model proposed in our previous work. However, it introduced computation overheads for deriving empirical distributions and performing iterative fitting. In this letter, we discuss how to greatly reduce the overheads for practical usage while maintaining denoising quality. For empirical distributions, a gridsubsampling strategy is adopted for acceleration. Regarding distribution fitting, two different methods are studied: equalfrequency merged distribution and L-moment fitting. The former reformulates the fitting process into entropy optimization for only few merged bins. It provides 6-13x speedup for model fitting with negligible quality loss and 9-20x speedup with ≤0.1 dB PSNR drop by using 20 and 10 bins respectively. The latter performs table lookup of L-moments, instead of conventional moments, for robust fitting of heavy-tailed distributions. The fitting time then becomes negligible with ≤0.2 dB drop in most cases, e.g. the overall run time for bilateral 9x9 filtering can be thus accelerated by around 6x. Experiments on bilateral and non-local means filters are also given to show the speedup, quality and robustness. Publications C.-T.
Huang, "Fast Distribution Fitting for Parameter Estimation of
Range-Weighted Neighborhood Filters,"
IEEE Signal
Processing Letters, vol. 23, no. 3, pp331-335, Mar 2016. Source Code For reproducing
the results for bilateral filters, which includes
grid-subsampled PMF derivation, EFM and L-moment fitting, and
fast image filtering (multicore processing and vectorization). |
|
Supplementary Data for Experimental Results Please click on the following link for the detailed fitting and filtering results: Note:
1. Best viewing resolution is 1920x1080. Otherwise, you
may need to zoom out the webpage for a good viewing experience. Acknowledgement This work was supported by the Ministry of Science and Technology, Taiwan, R.O.C. under Grant No. MOST 103-2218-E-007-008-MY3.
Last update on Jan 12, 2016 |