A new measure of the robustness of biochemical networks

Bor-Sen Chen, Yu-Chao Wang, Wei-Sheng Wu and Wen-Hsiung Li

Supplemental materials

Simulation experiment 2

Consider the glycolytic-glycogenolytic pathway in perfused rat liver (Scrutton and Utter, 1968; Torres, 1994). Glycolysis and glycogenolysis are central steps of carbonhydrate metabolism (White et al., 1968). They yield the common intermediate glucose-6-phosphate, which can subsequently be used by the organism as a major source of energy. The main route of glycogen utilization is glycogenolysis via glycogen phosphorolysis to glucose-1 phosphate and subsequent conversion to glucose-6-phosphate via the phosphoglucomutase reaction. Glucose-6-phosphate can be used for energy production or formation of glucose. It is clear that a detailed, quantitative understanding of the kinetic and dynamic properties of glucose, glycogen, and glucose-6-phosphate is central to any assessments of the energy economy of organisms and of diseases like diabetes that are associated with the balance and imbalance of carbohydrates (Voit, 2000). The kinetic properties of the pathway are obtained as follows (Voit, 2000), which are also shown in Figure S2

(29)

where

In this case, the system matrix is obtained as

The dynamic response of the nominal glycolytic-glycogenolytic pathway in (29) is given in Figure S3(a) and the upper bound of the tolerance is given by

That is, if the parameter perturbation measure is less than , i.e. the robustness matrix , the characteristics of the steady state will be preserved.

Suppose the glycolytic-glycogenolytic pathway suffers from a kinetic perturbation as follows

(30)

in which the parameter perturbation is of the following form

In this perturbed case, and , which is a positive definite matrix with

its eigenvalues all positive (i.e., 0.0204, 2.8261, 56.3208). From our computational result and the perturbed dynamic response shown in Figure S3(b), the robustness of steady state is preserved. Suppose another parameter perturbation occurs such that the glycolytic-glycogenolytic pathway is perturbed as

(31)

Remark S1: The perturbed pathway is based on the GMA model (Voit, 2000) to meet the constraints of the precursor-product relationships.

In this case, we have

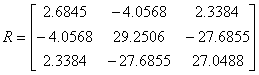is not positive definite, because its eigenvlaues are not all positive (i.e., -0.0915, 2.7967, 56.2427). Therefore, the

robustness condition is violated. From the dynamic response shown in Figure S3(c), we can see that the steady state of the biochemical network ceases to exist.

In order to confirm the compensatory parameter variations (i.e., for all i,j such that ) in Remark 2 of the text, let us consider the following compensatory parameter perturbations due to negative self-feedback regulation in metabolite X₂

(32)

In this high parameter perturbation case, the simulation result is shown in Figure S3(d). It is seen that the time response is almost the same as the nominal system at the steady state, though with some difference in the transient state. Obviously, the occurrence of compensatory perturbation due to negative self-feedback regulation is helpful for maintaining the robustness of biochemical networks.

Simulation experiment 3

The tricarboxylic acid (TCA) cycle in Dictyostelium, a soil-living amoeba, produces ATP very efficiently while decomposing pyruvate to water and CO₂ via acetyl-CoA. Under a nutrient-rich condition, the cycle is fed by ingested proteins that are broken down into amino acids. During the period of starvation, cellular proteins are used up (Newsholme, 1973; Voit, 2000). In this case, the TCA cycle model is simplified reasonably to involve the following 13 dependent metabolites and 26 enzyme-catalyzed process (Newsholme, 1973; Kelly et al., 1979; Voit, 2000).

The S-system model is shown as follows (Voit, 2000)

(33)

The TCA network in the above equation is shown in Figure S4, and the dynamic response is shown in Figure S5(a). The system matrix is obtained as

From , we can calculate the upper bound of the perturbation tolerance . That means when the network is perturbed by such that the robustness condition (14) is violated, and the steady state of the biochemical network may not exist. Suppose there is a perturbation as follows

(34)

where

In the perturbed case, the robustness matrix R is not a positive definite matrix with its eigenvalues (-0.006, 0.0218, 0.0955, 0.3666, 0.5360, 0.8629, 0.9511, 1.3141, 2.2116, 2.4675, 2.9605, 3.9098, 13.7447) and the dynamic response of the perturbed TCA cycle is shown in Figure S5(b). Obviously, the steady state of the perturbed TCA cycle ceases to exist.

Simulation experiment 4

Periodic responses are often encountered in organisms ranging from bacteria to mammals. A periodic oscillation can be considered as one kind of steady state phenomenon from the system point of view. A periodic network in Figure S6 is modeled as follows to produce the spontaneous oscillations in cAMP observed during the early development of D. discoideum (Laub and Loomis, 1998) and account for the synchronization of the cells necessary for chemotaxis (Yi et al., 2000; Ma and Iglesia, 2002).

From (14) or (15), we can find that if the perturbation measure is large such that the robustness condition is violated, the robustness of the steady state may not be preserved. Suppose the parameter perturbation as follows

In this case, all eigenvalues of R are greater than 0, and the oscillation still exists as shown in Figure S7(b). However, when the perturbation is as follows

the robustness condition is violated, i.e., the smallest eigenvalue of R is less than zero. The oscillation disappears and the steady state of the biochemical network ceases to exist as shown in Figure S7(c). Obviously, the proposed robustness measure is an important indicator of the robustness of biochemical networks under parameter perturbations.

REFERENCES

Kelly, P.J., Kelleher J.K. and Wright B.E. (1979) The tricarboxylic acid cycle in Dictyostelium discoideum. A model of the cycle at preculmination and aggregation. Biochem J., 184, 589-97.

Laub, M.T. and Loomis, W.F. (1998) A molecular network that produces spontaneous oscillations in excitable cells of dictyostelium. Mol. Biol. Cell, 9, 3521-3532.

Ma, L. and Iglesias, P.A. (2002) Quantifying robustness of biochemical network models. BMC Bioinformatics, 3:38, 1-13.

Newsholme, E.A. and Start, C. (1973) Regulation in Metabolism. pp. 69-76, Wiley, London.

Scrutton, M.C. and Utter, M.F. (1968) The regulation of glycolysis and gluconeogenesis in animal tissues. Annu. Rev. Biochem., 37, 249-303.

Torres, N.V. (1994) Modelization and experimental studies on the control of the glycolytic-glucogenolytic pathway in rat liver. Mol. Cell. Biochem., 132, 117-126 .

Voit, E.O. (2000) Computational analysis of biochemical system. Cambridge University Press, Cambridge.

White, A., Handler, P. and Smith, E.L. (1968) Principles of Biochemistry. 4th edition. McGraw-Hill, New York.

Yi, T.M., Hung, Y., Simon, M.I. and Doyle, J. (2000) Robust perfect adaptation in bacterial chemotaxis through intergral feedback control. Proc. Nat. Acad. Sci., 97, 4649-4653.

FIGURES